Bragg diffraction

Bragg diffraction (also referred to as the Bragg formulation of X-ray diffraction) was first proposed by William Lawrence Bragg and William Henry Bragg in 1913 in response to their discovery that crystalline solids produced surprising patterns of reflected X-rays (in contrast to that of, say, a liquid). They found that in these crystals, for certain specific wavelengths and incident angles, intense peaks of reflected radiation (known as Bragg peaks) were produced. The concept of Bragg diffraction applies equally to neutron diffraction and electron diffraction processes.

W. L. Bragg explained this result by modeling the crystal as a set of discrete parallel planes separated by a constant parameter d. It was proposed that the incident X-ray radiation would produce a Bragg peak if their reflections off the various planes interfered constructively.

The Bragg condition

Bragg diffraction occurs when electromagnetic radiation or subatomic particle waves with wavelength comparable to atomic spacings are incident upon a crystalline sample, scattered in a specular fashion by the atoms in the system, and undergo constructive interference in accordance to Bragg's law. For a crystalline solid, the waves are scattered from lattice planes separated by the interplanar distance d. Where the scattered waves interfere constructively; they remain in phase since the path length of each wave is equal to an integer multiple of the wavelength. The path difference between two waves undergoing constructive interference is given by

2dsinθ

, where θ is the scattering angle. This leads toBragg´s law which describes the condition for constructive interference from successive (h,k,l) of the crystalline lattice:

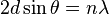
$\; 2 d\sin\theta = n\lambda$

Where n is an integer determined by the order given, and λ is the wavelength. A diffraction pattern is obtained by measuring the intensity of scattered waves as a function of scattering angle. Very strong intensities known as Bragg peaks are obtained in the diffraction pattern when scattered waves satisfy the Bragg condition.

Reciprocal space

More elegant is the description in reciprocal space. Reciprocal lattice vectors describe the set of lattice planes as a normal vector to this set with length

G = 2π / d .

Then Bragg's law is simply expressed by the conservation of momentum transfer

(G = k f - k i)

with incident and final wave vectors k_i and k_f of identical length. The precedent relation is also called laue difracttion and not only gives the absolute value, but a full vectorial description of the phenomenon. The scanning variable can be the length or the direction of the incident or exit wave vectors relating to energy- and angle-dispersive setups. The simple relationship between diffraction angle and Q-space is then.

$Q = \frac {4 \pi \sin \left ( \theta \right )}{\lambda} .$

Selection rules and practical crystallography

Bragg's law, as stated above, can be used to obtain the lattice spacing of a particular cubic system through the following relation:

$d = \frac{a}{ \sqrt{h^2 + k^2 + l^2}}$

where

a

is the lattice spacing of the cubic crystal, and

h

k

, and

l

are the Miller indices of the Bragg plane. Combining this relation with Bragg's law.

One can derive selection rules for the Miller indices for different cubic Bravais lattices; here, selection rules for several will be given as is.

Nobel Prize for Bragg diffraction

In 1915, William Henry Bragg and William Lawrence Bragg were awarded the Nobel Prize for their contributions to crystal structure analysis. They were the first and (so far) the only father-son team to have jointly won the prize. Other father/son laureates include Niels and Aage Bohr, Manne and Kai Siegbahn, J. J. Thomson and George Thomson, Hans von Euler-Chelpin and Ulf von Euler, and Arthur and Roger Kornberg, who were all awarded the prize for separate contributions.

We can think of the crystal as being composed of thousands of mirrors that reflect the X-rays. These "mirrors" are called Bragg planes. When light is reflected from a mirror, the angle of incidence (the angle at which it strikes the plane of the mirror) is equal to the angle of reflection. The same is true of Bragg planes, and the reason is that when the angle of incidence is equal to the angle of reflection, light rays hitting the plane (mirror) in phase exit in phase, regardless of where they hit the mirror. Notice, by the way, that the incoming and outgoing rays differ in direction by a total angle of 2θ. If rays reflected from a plane have identical pathlengths, then rays reflected from different planes must have different pathlengths. We can easily work out how far apart the planes must be for the difference in pathlength to be equal to the wavelength of the incoming radiation, so that the scattered rays from the two planes would again be in phase. It turns out that the difference in pathlength depends on the angle of incidence (and reflection). The image below shows how to work out the relationship, which is called Bragg's law.

The difference in pathlength between the rays reflected from the two planes is twice the distance l. Simple geometry tells us that the upper angle in the little triangle must be q, because the sum of the angles inside a triangle is 180 degrees, and the other two angles are 90 degrees and 90-θ. Then simple trigonometry tells us that the distance l is equal to d sinθ. For the two rays to be diffracted in phase, twice l must be equal to the wavelength, so we have the relationship:

λ = 2 d sinθ

In Bragg's law, as the angle increases, d must become smaller for the pathlength to remain equal to one wavelength. We can show this by various common rearrangements of the equation:

sinθ/λ = 1/(2 d)

d = λ/ (2 sinθ)

We can obtain same phase of different waves by calculating the optical path deference between two waves. If we want that two waves will have the same phase and will get maximum intensity we need that the condition that the relative phase will be a multiple of 2π :

2dsinθ=λm

If we want that the intensity of the diffracting waves will be 0 we need to demand Δφ=π so the optical path deference between two waves will satisfy the condition:

2dsinθ=λ(m+1/2)

Finally ,in the general case we have the condition that the optical path deference between two waves will be arbitrary angel:

2dsinθ=λ(m+Δφ/(2π))

the Bragg scattering from two Bragg planes can be visualize in the function: scanning_angels_func(h,f,d_teta,final_teta) ,which can be downloaded in the download section. Here we can see an example of waves diffracting in phase for cubic latice with a=3 and wave with λ=3 : An example of waves diffracting in of phase

An example of waves diffracting out of phase

Von Laue condition for scattering and Ewald construction

Ewald came up with a geometrical construction to help visualize which Bragg planes are in the correct orientation to diffract. In the Ewald sphere, we have two origins (which can make you uncomfortable until you realize that it is just a geometrical construction that makes the mathematics of diffraction easy to picture). The origin of the crystal is at the center of the Ewald sphere, and the incoming X-rays are diffracted from that crystal. The origin of reciprocal space is at the point where the incoming X-ray beam would exit the Ewald sphere. If we rotate the crystal, we rotate the Bragg planes and so we rotat

Direct lattice and reciprocal lattice

A typical direct Bravis lattice vector in 2D can be written as : R=n1a +n2b ,where a,b are the direct lattice primitive unit cell vectors.
The typical reciprocal lattice vector can be written as: G=kA+hB , where A,B are the reciprocal lattice primitive unit cell vectors.
The relation between the direct lattice primitive unit cell vectors and the reciprocal lattice primitive unit cell vector : A=2π/D(by,-bx) , B=2π/D(ay,-ax)
The relation between direct lattice vector R and reciprocal lattice vector G: eiGR=1 From the last relation we can see that R and G are vertical.
We describe Bragg planes with the direct lattice vector R and or with the reciprocal lattice vector G and the relation between the indexes n,m,k and h is : n:m=1/k:1/h.
We can write Bragg law 2dsinθ=λm in terms of G and k (k=2π/λ): 2ksinθ=Gm.
Notice that if we take two G vectors with the same relation between k and h (for example-G1=(1,1), G2=(2,2) ),the distance between two Bragg planes d is calculated according to the smallest G vector, but the other G vector also satisfies the Bragg equation but for higher order n.
We define K as the vector of the incoming wave and K' as the vector of the outgoing wave and their relation with G as: G=K'-K or G=2ksinθ. definitions:
reciprocal latice:-in SC(Simple cubic)the recuiprocal latice looks ezactly like the real latice in change of the atoms scale G vector-G vector is difined as and it always "nizav" to the bragg plane which the scattering is taking place. the realion between G K and K':
the reciprocal space in the same direction. Since diffraction from a crystal is confined to points on the reciprocal lattice (corresponding to planes that can be specified by integer indices), we can think of rotating the reciprocal lattice when we rotate the crystal. The following figure shows this schematically, illustrating planes of points in the reciprocal lattice. The planes of points in the reciprocal lattice intersect the Ewald sphere to give a circle of points in the diffracting condition. When the planes are aligned perpendicular to the X-ray beam, these circles on the Ewald sphere will project onto circles of spots surrounding the direct beam position but, as we rotate the crystal (and the reciprocal lattice) the circles on the Ewald sphere will be distorted and will project into what are called lines of spots.

When executing the function ewald(k), which can be downloaded in the download section, we can see selection of Bragg planes and representations of vectors G K and K' in the reciprocal lattice (lower right window), Bragg planes and waves phases(upper left window), and the interference phase(upper right window).

Here are some examples of Bragg scattering from different planes: