Reciprocal Lattice

DEFINITION:

The reciprocal space lattice is a set of imaginary points constructed in such a way that the direction of a vector from one point to another coincides with the direction of a normal to the real space planes and the separation of those points (absolute value of the vector) is equal to the reciprocal of the real interplanar distance.

Any repetitive and periodic distribution of an object (or motif) can be characterized, or described, by the translations that repeat the object periodically. This set of translations generate what we call a direct lattice.

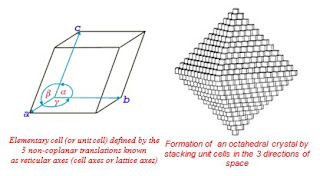
The translations that describe the periodicity in crystals can be expressed as a linear combination of three basic translations, not coplanar, ie independent, known as reticular or lattice axes (or unit cell axes). These axes define a parallelogram (in 2 dimensions), or a parallelepiped (in 3 dimensions) known as a unit cell(or elementary cell). This elementary area (in 2-dimensional cases), or elementary volume (in 3-dimensional cases), which holds the minimum set of the periodic distribution, generates (by translations) the full distribution which, in our 3-dimensional case, we call crystal.

In general, inside the unit cell there is a minimum set of atoms (ions or molecules) which are repeated inside the cell due to the symmetry elements of the crystal structure. This minimum set of atoms (ions or molecules) which generate the whole contents of the unit cell (after applying the symmetry elements to them) is known as the asymmetric unit.

The lattice, which is a purely mathematical concept, can be selected in various ways in the same real periodic distribution. However, only one of these lattices "fits" best with the symmetry of the periodic distribution of the motifs.

As is shown in the left figure above, any lattice that describes the repetition of the motif (triangle + circle) can be decomposed into two identical equivalent lattices (one for each object of the motif). Thus, the concept of lattice is independent of the complexity of the motif, so that we can use only one lattice, since it represents all the remaining equivalent ones.

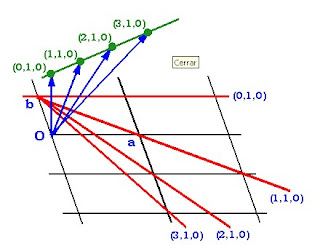
Once we have chosen a representative lattice, appropriate to the symmetry of the structure, any reticular point (or lattice node) can be described by a vector that is a linear combination (with integer numbers) of the direct reticular axes: R = m a + n b + p c, where m, n and p are integers. Non-reticular points can be reached using the nearest R vector, and adding to it the corresponding fractions of the reticular axes to reach it:

r = R + r' = (m a + n b + p c) + (x a + y b + z c) Position vector for any non-reticular point of a direct lattice

where x, y, z represent the corresponding dimensionless fractions of axes X/a, Y/b, Z/c, and X, Y, Z the corresponding lengths.

From a geometric point of view, on a lattice we can consider some reticular lines and reticular planes which are those passing through the reticular points (or reticular nodes).

Just as we did with the lattices (choosing only one of them from all the equivalent ones), we do the same with the reticular lines and planes. A reticular line or a reticular plane can be used as a representative of the entire family of parallel lines or parallel planes.

A unique plane, as the one drawn in the top right figure, defined by the numerical triplet known as Miller indices, represents and describes the whole family of parallel planes passing through every element of the motif. Thus, in a crystal structure, there will be as many plane families as possible numerical triplets exist with the condition that these numbers are primes, one to each other (not having a common divisor). The Miller indices are generically represented by the triplet of letters hkl.

If there are common divisors among the Miller indices, the numerical triplet would represent a single family of planes only. For example, the family with indices (330), which are not strictly reticular, can be regarded as the representative of 3 families of indices (110) with a geometric out-of-phase distance (among the families) of 1/3 of the original (see the figures below).

Thus, the concept of Miller indices, previously restricted to numerical triplets (being prime numbers), can now be generalized to any triplet of integers. In this way, every family of planes, will "cover" the whole crystal. And therefore, for every point of the crystal we can draw an infinite number of plane families with infinite orientations.

Of course, interplanar spacings can be directly calculated from the Miller indices (hkl) and the values of the reticular parameters (unit cell axes). The table below shows that these relations can be simplified for the corresponding metric of the different lattices.

Any plane can also be characterized by a vector (σ_hkl) perpendicular to it. Therefore, the projection of the position vector of any point (belonging to the plane), over that perpendicular line is constant and independent of the point. It is the distance of the plane to the origin, ie, the spacing (d_hkl ).

If from this normal vector σ_hkl of length 1/d_hkl, we take another vector, n times (integer) longer (n.σ_hkl), the above mentioned product (|σ_hkl| d_hkl = 1) would imply that the new vector (n.σ_hkl) will correspond to a family of planes of indices nh,nk,nl having an interplanar spacing n times smaller.

Therefore, it appears that the moduli (lengths) of the perpendicular vectors (σ_hkl) are reciprocal to the interplanar spacings. The end points of these vectors also produce a periodic lattice that, due to this reciprocal property, is known as the reciprocal lattice of the original direct lattice. The reciprocal points, obtained in this way, are identified with the same numerical triplets hkl (Miller indices) which represent the corresponding plane family.

Geometrical construction of some points of a reciprocal lattice (green points) from a direct lattice. To simplify, we assume that the third axis of the direct lattice (c) is pependicular to the screen. The red lines represent the reticular planes (perpendicular to the screen) and whose Miller indices are shown in blue. As an example: the reciprocal point with indices (3,1,0) will be located on a vector perpendicular to the plane (3,1,0) and its distance to the origin O is inversely proportional to the spacing of that family of planes.

It should now be clear that the direct lattice, and its reticular planes, are directly associated (linked) with the reciprocal lattice. Moreover, in this reciprocal lattice we can also define a unit cell (reciprocal unit cell) whose periodic translations will be determined by three reciprocal axes that form reciprocal angles among them.

ORLANING COLMENARES

ELECTRONICA DEL ESTADO SOLIDO

C.I.V.- 18.991.089

Visita mi BLOG: http://orlaningsolidstate.blogspot.com

---

Explore the seven wonders of the world Learn more!